We know that all scalar fields posses isosurfaces. “An isosurface is the locus of all points in space, which posses same value of scalar field”. Consider a field ![]() . Let
. Let ![]() and
and ![]() represent two closely separated isosurfaces of the field
represent two closely separated isosurfaces of the field ![]() . Let the value of scalar field at all points on isosurface
. Let the value of scalar field at all points on isosurface ![]() is
is ![]() and the value of filed at all points on isosurface
and the value of filed at all points on isosurface ![]() is
is ![]() as shown in Fig. 1
as shown in Fig. 1
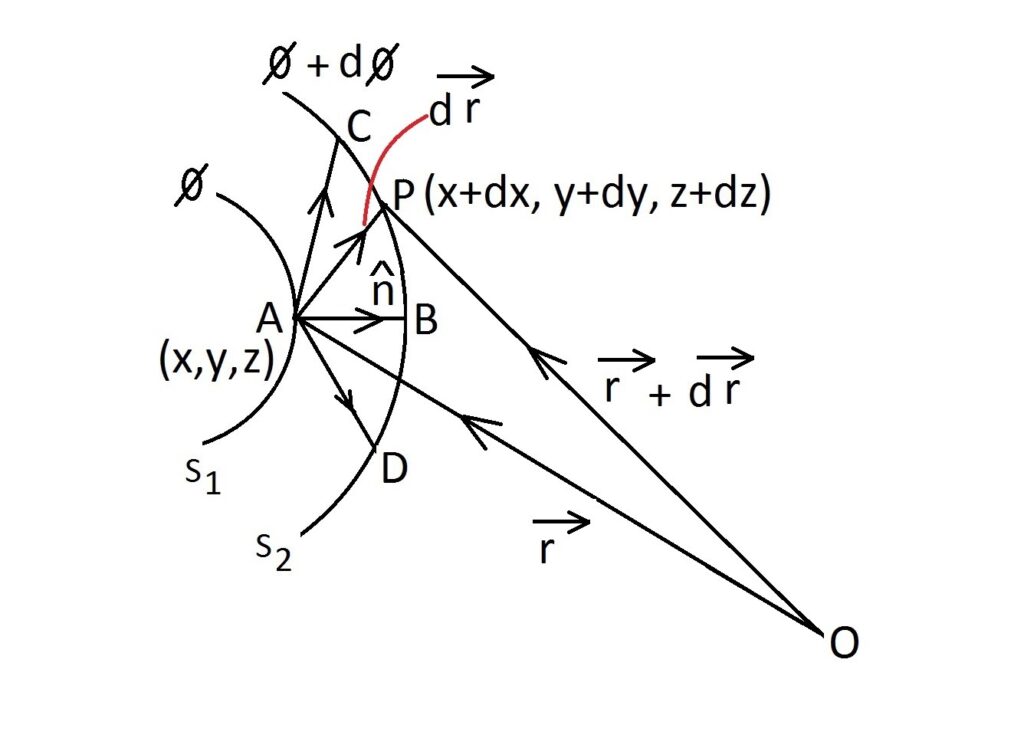
Consider any point ![]() on isosurface
on isosurface ![]() and any point
and any point ![]() on isosurface
on isosurface ![]() . Let
. Let ![]() and
and ![]() be the position vectors of the points A and P respectively. Therefore, by triangle law of vectors, the displacement
be the position vectors of the points A and P respectively. Therefore, by triangle law of vectors, the displacement ![]() is given as follows:
is given as follows:
![]()
![]()
(1) ![]()
The magnitude of this displacement is given as follows:
(2) ![]()
The gradient of scalar field is given according to the following relation:
(3) ![]()
Since ![]() is a scalar field (function), therefore, the net change in the value of scalar field
is a scalar field (function), therefore, the net change in the value of scalar field ![]() in going from point A on isosurface
in going from point A on isosurface ![]() to some arbitrary point P on the isosurface
to some arbitrary point P on the isosurface ![]() is given by:
is given by:
(4) ![]()
From calculus, we know that ![]() represents the rate at which scalar
represents the rate at which scalar ![]() changes along X-axis, keeping the y, z as constants. Therefore, change in
changes along X-axis, keeping the y, z as constants. Therefore, change in ![]() due to net displacement
due to net displacement ![]() (X-component of the displacement
(X-component of the displacement ![]() ) along X-axis in going from A to P is given by:
) along X-axis in going from A to P is given by:
![]()
Similarly, we can write:
![]()
![]()
Since ![]() , therefore, It can be easily understood that:
, therefore, It can be easily understood that:
Change in ![]() along displacement
along displacement ![]()
![]()
![]()
![]()
(5) ![]()
Comparing equations (4) and ( 5), we get the following relation:
(6) ![]()
Important Note:
Consider two vectors ![]() and
and ![]() such that
such that
![]()
and
![]()
and ![]() is the angle between the vectors. Therefore, dot product of two vectors is given by following expressions:
is the angle between the vectors. Therefore, dot product of two vectors is given by following expressions:
![]()
and
![]()
Equation (6) can also be written as follows:
![]()
(7) ![]()
[Using equations (1) and ( 6)]
Let ![]() is the angle between the vectors
is the angle between the vectors ![]() and
and ![]() , then above equation can be simplified as follows:
, then above equation can be simplified as follows:
(8) 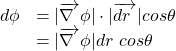
(9) ![]()
The left side of the equation (9) represents rate of change of ![]() with respect to position of a point along the path AP (see Fig. 1). It is clear that this rate is always less than or equal to the magnitude of gradient of scalar field, that is
with respect to position of a point along the path AP (see Fig. 1). It is clear that this rate is always less than or equal to the magnitude of gradient of scalar field, that is ![]() (because value of
(because value of ![]() is always less than or equal to 1). Therefore, it is clear that derivative of a scalar quantity / function / field with respect to position is not always equal to gradient magnitude. This equality comes only under one condition that the value of
is always less than or equal to 1). Therefore, it is clear that derivative of a scalar quantity / function / field with respect to position is not always equal to gradient magnitude. This equality comes only under one condition that the value of ![]() must be equal to 1. When such condition is met, then the rate
must be equal to 1. When such condition is met, then the rate ![]() is maximum and it is written as
is maximum and it is written as ![]() . That is
. That is
![]()
![]()
Under this condition, equation (9) will become:
(10) ![]()
(11) 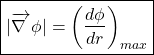
From equation (11), we can write the physical significance of gradient of a scalar field as follows:
“The magnitude of gradient of scalar field at a point is equal to the maximum rate of change of field with respect to the position.”
The only task remaining is to find the direction of gradient; as the equation (11) only gives its magnitude. To accomplish this, we turn our attention to the Fig. 1. Note that the direction of ![]() is along the path AP. P is arbitrary point on the isosurface
is along the path AP. P is arbitrary point on the isosurface ![]() . Therefore, AP represents all possible displacements from point A on isosurface
. Therefore, AP represents all possible displacements from point A on isosurface ![]() to all points on the isosurface
to all points on the isosurface ![]() . A few paths from
. A few paths from ![]() to
to ![]() are shown in Fig. 1, like paths AB, AC and AD.
are shown in Fig. 1, like paths AB, AC and AD.
It is clear that along all these paths, the starting point is on isosurface ![]() and end point is on isosurface
and end point is on isosurface ![]() . Therefore, change in the field
. Therefore, change in the field ![]() along all these paths is essentially
along all these paths is essentially ![]() , however, the path lengths or magnitude of displacements (
, however, the path lengths or magnitude of displacements (![]() ) along these paths are not same. It means that, for the rate expression
) along these paths are not same. It means that, for the rate expression ![]() the value of numerator is same, but the value of denominator is different along all these paths. Therefore, the rate
the value of numerator is same, but the value of denominator is different along all these paths. Therefore, the rate ![]() will be maximum along the shortest path (because denominator
will be maximum along the shortest path (because denominator ![]() will be minimum). But it is clear that the shortest path is AB and the displacement
will be minimum). But it is clear that the shortest path is AB and the displacement ![]() is along the normal to the isosurface
is along the normal to the isosurface ![]() .
.
Let ![]() is unit vector along the normal to point A on isosurface
is unit vector along the normal to point A on isosurface ![]() . Therefore
. Therefore
![]()
Moreover along path AB,
![]()
and
![]()
It is also clear that along path AB we have ![]() , that is
, that is ![]() . It means that along the shortest path, the direction of displacement vector and gradient vector are same. Since the direction of shortest displacement is along the normal vector (
. It means that along the shortest path, the direction of displacement vector and gradient vector are same. Since the direction of shortest displacement is along the normal vector (![]() ), therefore, the direction of gradient vector is also along the normal vector to isosurface defined by scalar field. Hence we can write:
), therefore, the direction of gradient vector is also along the normal vector to isosurface defined by scalar field. Hence we can write:
![]()
![]()
[Using equation (11)]
(12) 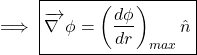
Thus complete physical significance of gradient of a scalar field can be stated as follows:
“Gradient of a scalar field at a point represents the maximum rate of change of scalar field with respect to position and it is always directed along the normal to the field surface at that point.”
Due to the reason that gradient of a scalar field is always directed along the normal direction, it is also called as directional derivative of a scalar field.

OK sir , thanks for your good presentation. My question is that Gradient is Perpendicular to isosurface is fine. But being normal it can point outward or inward to the surface. How to determine this?
thanks in advanve