Let ![]() is a scalar field, which is a function of space variables
is a scalar field, which is a function of space variables ![]() . Then the gradient of scalar field is defined as operation of
. Then the gradient of scalar field is defined as operation of ![]() on the scalar field.
on the scalar field.
That is:
![]() =
= ![]()
![]()
Here the operator ![]() is called Del or Nabla vector. It is given by the following expression:
is called Del or Nabla vector. It is given by the following expression:
(1) ![]()
Please note that ![]() and
and ![]() are unit vectors along X, Y and Z axes respectively in cartesian system of cordinates.
are unit vectors along X, Y and Z axes respectively in cartesian system of cordinates.
Thus using the description given in Eq: (1), the expression for gradient of a scalar field can also be written as:
![]() =
= ![]()
![]() =
= ![]()
![]()
Example: 1 If ![]() is the position vector of a point (x, y, z) in space, then find the gradient of
is the position vector of a point (x, y, z) in space, then find the gradient of ![]() .
.
Solution: Since ![]() is the position vector of a point (x, y, z) in space, therefore, it is given as follows:
is the position vector of a point (x, y, z) in space, therefore, it is given as follows:
![]()
The magnitude of this vector is given as follows:
(2) ![]()
(3) ![]()
(4) ![]()
Let us now evaluate each term on the right hand side of equation (4) one by one and then solve the problem.
The first term can be calculated using equation (3) as follows:
(5) 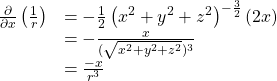
(using equation (2))
Similarly, we can find that
(6) ![]()
(7) ![]()
Put the values from equations (5), (6) and (7) in equation (4), we get
(8) ![]()
![Rendered by QuickLaTeX.com \[\implies\boxed{\overrightarrow\nabla\left(\frac{1}{r}\right) = -\frac{\overrightarrow{r}}{r^{3}}}\]](https://physicshut.com/wp-content/ql-cache/quicklatex.com-65e43e93ef09c72cdea5a5db50cdaf18_l3.png)
Example:2 If ![]() and
and ![]() be the position vectors of points
be the position vectors of points ![]() and
and ![]() in space, then find the gradient of
in space, then find the gradient of ![]() .
.
Solution: Since ![]() is the position vector of a point (x, y, z) in space, therefore, it is given as follows:
is the position vector of a point (x, y, z) in space, therefore, it is given as follows:
![]()
Similarly
![]()
Therefore
![]()
The magnitude of this difference or displacement vector is given by:
(9) ![]()
(10) ![]()
(11) ![]()
Let us now evaluate each term on the right hand side of equation (11) one by one and then solve the problem.
The first term can be calculated using equation (10) as follows:
(12) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{ll} \frac{\partial}{\partial x}\left(\frac{1}{|\overrightarrow{r~}-\overrightarrow {r~}'|}\right) &=-\frac{1}{2}\left({(x-x')}^2+{(y-y')}^2+{(z-z')}^2\right)^{-\frac{3}{2}}[2(x-x')]\\ &=\frac{-(x-x')}{(\sqrt{(x-x')^2+(y-y')^2+(z-z')^2})^{3}}\\ &=\frac{-(x-x')}{|\overrightarrow{r~}-\overrightarrow {r~}'|^{3}} \end{array} \end{equation*}](https://physicshut.com/wp-content/ql-cache/quicklatex.com-f990ddeca54fea02823efe56dd21a8df_l3.png)
(using equation (9))
Similarly, we can find that
(13) ![]()
(14) ![]()
Put the values from equations (12), (13) and (14) in equation (11), we get
(15) ![]()
(16) 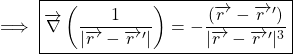
Example: 3 If ![]() and
and ![]() be the position vectors of points
be the position vectors of points ![]() and
and ![]() in space, then find the gradient of
in space, then find the gradient of ![]() with respect to the point
with respect to the point ![]() . That is, find expression for
. That is, find expression for ![]()
Solution: Since ![]() is the position vector of a point (x, y, z) in space, therefore, it is given as follows:
is the position vector of a point (x, y, z) in space, therefore, it is given as follows:
![]()
Similarly
![]()
Therefore
![]()
The magnitude of this difference or displacement vector is given by:
(17) ![]()
(18) ![]()
The gradient of ![]() with respect to the point
with respect to the point ![]() is given by:
is given by:
(19) ![]()
Let us now evaluate each term on the right hand side of equation (19) one by one and then solve the problem.
The first term can be calculated using equation (18) as follows:
(20) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{ll} \frac{\partial}{\partial x'}\left(\frac{1}{|\overrightarrow{r~}-\overrightarrow {r~}'|}\right) &=-\frac{1}{2}\left({(x-x')}^2+{(y-y')}^2+{(z-z')}^2\right)^{-\frac{3}{2}}[2(x-x')(-1)]\\ &=\frac{(x-x')}{(\sqrt{(x-x')^2+(y-y')^2+(z-z')^2})^{3}}\\ &=\frac{(x-x')}{|\overrightarrow{r~}-\overrightarrow {r~}'|^{3}} \end{array} \end{equation*}](https://physicshut.com/wp-content/ql-cache/quicklatex.com-6018113f6b0157e07fadf0e47a858915_l3.png)
(using equation (17))
Similarly, we can find that
(21) ![]()
(22) ![]()
Put the values from equations (20), (21) and (22) in equation (19), we get
(23) ![]()
(24) 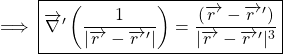
Example: 4 If ![]() and
and ![]() be the position vectors of points
be the position vectors of points ![]() and
and ![]() in space, then find the gradient of
in space, then find the gradient of ![]() with respect to the points
with respect to the points ![]() and
and ![]() . That is, find expression for
. That is, find expression for ![]() and
and ![]() . Hence show that these two gradients are equal and opposite. That is
. Hence show that these two gradients are equal and opposite. That is ![]()
Solution: We have already proved in Example 2 and Example 3 that
(25) ![]()
(26) ![]()
Comparing equations (25) and (26), we get the desired result. That is
![Rendered by QuickLaTeX.com \[\boxed{\overrightarrow\nabla'\left(\frac{1}{|\overrightarrow{r~}-\overrightarrow {r~}'|}\right)=-\overrightarrow\nabla\left(\frac{1}{|\overrightarrow{r~}-\overrightarrow {r~}'|}\right)}\]](https://physicshut.com/wp-content/ql-cache/quicklatex.com-281dd3dbcece56e399057c89382c9c0a_l3.png)
Note: This relation is very useful in the derivation and solution of many complex problems of electromagnetism.
If you are interested to know more about scalar and vector fields, then watch video lecture by me on this topic at the following link: https://youtu.be/H4eWdwaGWYI.
Another video, that may be of interest to the reader of this post is ‘Transverse nature of electromagnetic waves’. The link to this video lecture by me is given here: https://youtu.be/k7399IiFEzo
